高校生の皆さんへ・授業について
■科目名:知的制御(担当:伊藤 一之 教授)
◎ 授業の概要
ロボットおよびコンピュータに学習能力を持たせるための方法について学びます。講義形式で学習のアルゴリズムを学ぶだけでなく、各自が実際にプログラミングを行い、コンピュータが学習を行う様子を観察します。
◎ 授業内容
第 01-03回 【制御の基礎】
PD制御をはじめとする一般的な制御方法について復習する
第 04-07回 【知的制御】
強化学習、サブサンプションアーキテクチャなど,さまざまな知的制御について概要を解説する。
第 08 回 【強化学習】
強化学習のアルゴリズムについて解説する。
第 09-12回 【強化学習の実装】
EXCELのVBAを用いて強化学習を実装する。
第12-15回 【総合演習】
強化学習を用いて、仮想空間で自律的に振舞うロボットの制御を行う。
■科目名:制御工学(担当:伊藤 一之 教授)
◎ 授業の概要
制御工学は、産業用ロボットから、自動車、化学プラント、電化製品にいたるまで、非常に多くの分野で使用されています。本授業では、制御対象を物理学および数学を用いて記述し、これを所望の状態に制御するための制御系の設計方法について学びます。また、コンピュータを用いてシミュレーションを行い、各自が設計した制御系の性能を確認します。
◎ 授業内容
第 01 回 【概要】
制御工学の分類、歴史、展望を考察する。
第 02-04 回 【伝達関数とブロック線図】
動的システムを伝達関数とブロック線図を用いて表現する方法を学ぶ。
第 05-06 回 【MATLAB基礎】
MATLABを用いてシステムの応答をシミュレーションするための方法を学ぶ。
第 07-08 回 【基本伝達関数】
基本伝達関数の応答をMATLABを用いて確認する。
第 09-10 回 【フィードバック制御系の定常特性解析】
フィードバック制御系の定常特性の計算法とその意味を理解する。
第 11-12 回 【演習1】
(P制御,PD制御,PID制御) MATLAB Simulinkを用いてP制御,PD制御,PID制御の応答を求め,安定性,定常偏差,オーバーシュートなど,制御系の特性を理解する。
第 13-15 回 【演習2】
PIDコントローラのチューニング ステップ応答法および限界感度法を用いてPIDコントローラのチューニングを行う。
■科目名:光デバイス工学(担当:山内 潤治 教授)
◎ 授業の概要
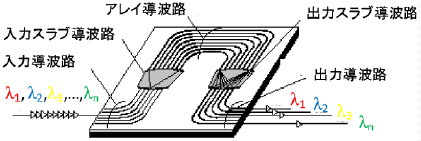
インターネットの爆発的な発展には、各種光デバイスが貢献しています。また、光に関する技術は、光通信のみならず、光情報処理や、最近話題となっている光センサなどにも応用されます。こうした各種光デバイスの動作原理と応用を学習します。光通信では、1本のファイバで多くの人の信号を伝送する必要があります。そこで、波長を少しずつ変えた光に信号をのせています。したがって、波長がわずかに異なる光を合波したり、分波したりするデバイスが必要不可欠となります。一例が、図に示す、アレイ導波路を利用した波長分割用デバイスです。屈曲した多くの導波路を配列して、波長多重を実現しています。動作特性を向上させる方法を学習します。
◎ 授業内容
| 第 01 回 | 電磁波伝送路の基礎 平行導体板の固有値問題、遮断波長 |
|---|---|
| 第 02 回 | 金属伝送路 同軸ケーブル、金属導波管、基本モード、高次モード |
| 第 03 回 | 光通信の概要 歴史的背景と現状の技術 |
| 第 04 回 | 光源 レーザ、発光ダイオード |
| 第 05 回 | 誘電体伝送路 TEモード、TMモード、屈折率分布による分類 |
| 第 06 回 | スラブ伝送路 屈折率分布による分類 |
| 第 07 回 | 光集積回路1 屈曲導波路、パワー分配器 |
| 第 08 回 | 光集積回路2 波長分割器、AWG |
| 第 09 回 | 光集積回路3 フィルタ、変調器 |
| 第 10 回 | 光集積回路4 スイッチ、メモリ |
| 第 11 回 | 光集積回路5 ビームの偏向、非線形導波路の応用 |
| 第 12 回 | 光ファイバ通信1 光ファイバケーブル、LPモード、損失特性 |
| 第 13 回 | 光ファイバ通信2 分散特性、符号誤り率、波長多重技術 |
| 第 14 回 | 光情報処理 空間周波数フィルタリング、ホログラフィ |
| 第 15 回 | 総まとめ 重要点の整理 |
■科目名:基礎電気回路(担当:斎藤 利通 教授)
◎ 授業の概要
スマートホン、太陽光発電、インターネットなど様々な電気電子工学の技術を実現するためには、高性能の電気電子回路を設計する必要があり、この科目はそのための第一歩です。抵抗、キャパシタ、インダクタ、電源等で構成された基本的な回路の動作―各部の電圧、電流、電力のふるまい―を解析する方法を学びます。その解析のためには、数学で学んだ様々な基礎事項の工学的意義を理解することがとても重要です。例えば、高校では幾何などの問題を解くために使っていた三角関数は、大学の回路工学では、音声や画像信号を表現し、通信する技術を構築するために巧みに使われます。
◎ 授業内容
| 第 01 回 | 導入 意義と動機づけ |
|---|---|
| 第 02 回 | 抵抗回路網 導入、変数(枝電流、枝電流)、キルヒホッフの法則、電源の変換 |
| 第 03 回 | 抵抗回路網 抵抗とコンダクタンス, 節点電圧、節点方程式 |
| 第 04 回 | 抵抗回路網 ループ電流、網路方程式、混合解析 |
| 第 05 回 | 抵抗回路網 重ねの理、テブナン-ノートンの等価回路 |
| 第 06 回 | ダイナミック回路 キャパシタとインダクタ、接続、エネルギー |
| 第 07 回 | ダイナミック回路 RC回路, RL回路、平衡点と時定数 |
| 第 08 回 | ダイナミック回路 複素数とオイラーの公式、RLC回路 |
| 第 09 回 | ダイナミック回路 ラプラス変換、部分分数、RC回路とRLC回路 |
| 第 10 回 | ダイナミック回路 プラス変換、複素-部分分数、DC定常解、回路の初期値 |
| 第 11 回 | 正弦波正常状態 複素数、指数表示、フェーザ |
| 第 12 回 | 正弦波定常状態 フェーザ法による回路方程式定常解の解法 |
| 第 13 回 | 正弦波定常状態 インピーダンスとアドミッタンス、節点網路解析 |
| 第 14 回 | 正弦波定常状態 重ねの理, 共振回路 |
| 第 15 回 | 総復習 重要事項の再説明と基本的な演習問題の解説 |
■科目名:基礎アナログ電子回路(担当:安田 彰 教授)
◎ 授業の概要
電子回路は、身の回りの電気製品のみならずさまざまな工業製品の中で用いられています。本講座では、電子回路の特徴であるトランジスタなどの能動素子を用いた回路の特徴、解析方法、設計方法について学びます。また、授業では実際のトランジスタを用いた実験を通して回路動作の理解を深めます。
◎ 授業内容
| 第 01 回 | 受動素子 抵抗,キャパシタ,インダクタ,電源,制御電源 |
|---|---|
| 第 02 回 | 電子管および半導体 電子管,共有結合と半導体,不純物半導体,pn接合とダイオード,ダイオード特性と等価回路 |
| 第 03 回 | トランジスタの基本特性1 npn接合とpnp接合,トランジスタの動作と静特性,電流増幅率(α,β) |
| 第 04 回 | トランジスタの基本特性2 FET, MOS FETno動作と静特性 |
| 第 05 回 | トランジスタの小信号等価回路 トランジスタの小信号等価回路の導出 |
| 第 06 回 | トランジスタを用いた基本回路1 回路の諸特性,バイアス回路,エミッタ接地回路 |
| 第 07 回 | トランジスタを用いた基本回路2 ベース接地回路,コレクタ接地回路 |
| 第 08 回 | トランジスタを用いた基本回路の実験 エミッタ接地回路の動作実験 |
| 第 09 回 | トランジスタを用いた基本回路3 2つのトランジスタを使った基本回路と特性 |
| 第 10 回 | Spiceによるシミュレーション 基本回路のSpiceによるシミュレーション |
| 第 11 回 | 差動増幅回路1 トランジスタ差動増幅回路の構成,大信号特性,小信号等価回路 |
| 第 12 回 | 差動増幅回路2 差動利得,同相利得および同相成分抑圧比とその改善法 |
| 第 13 回 | カレントミラー回路 カレントミラー回路の構成と特性 |
| 第 14 回 | 能動負荷を用いた増幅器 能動負荷を用いた増幅器の構成と特性 |
| 第 15 回 | まとめ |
■科目名:電気電子工学入門(担当:安田 彰 教授)
◎ 授業の概要
古代ギリシャ時代の静電気の発見から、18世紀から始まる近代電気電子工学の発展をその歴史と共に学びます。また、20世紀から21世紀に急速に発展したこれらの基礎技術やその応用分野を身近な製品などを例に概説します。
◎ 授業内容
| 第 01 回 | 身の回りの電気 身の回りで使われている電子機器類をあげ,それらに使われている技術,関連する学問について説明する |
|---|---|
| 第 02 回 | 【電気の歴史】 有史以来,我々が用いてきた電気に関する知識や応用,関連する学問について概説する |
| 第 03 回 | 20世紀および21世紀における発展 21世紀の現代までにおける電気に関する学問の歴史を概説する.特に20世紀において電気関連の学問は急速に発展したが,この時代における発見,発明を中心に,これらが現在の技術とどう結びついているか考察する。 |
| 第 04 回 | 【電子デバイスI】 真空管および半導体に至る能動素子の開発の歴史およびその基本原理について概説する |
| 第 05 回 | 【電子デバイスII】 現代の半導体デバイスについて概説する.特にシリコンCMOSトランジスタの原理,製造方法,特性,応用例について学ぶ。 |
| 第 06 回 | 【電子回路デザイン】 基本的な回路デザインについて概説する.回路デザインに必要な回路理論の基本を説明し,その大系をつかむ.次に,トランジスタ1つの回路を例に素子の特性を活かした回路デザイン方法を学ぶ。 |
| 第 07 回 | 【通信システムI】 古代からの通信の方法について紹介し,有線電信,無線電信,無線通信と現代にいたる通信システムの歴史およびその基本原理について概説する。 |
| 第 08 回 | 【通信システムII】 現代の通信システムについて概説する.携帯電話を例に,そこで使われている技術(無線通信,変復調,デジタル信号処理)を解説し,電気電子工学科で学ぶ科目との関係を示す。 |
| 第 09 回 | 【コンピュータI】 計算機の歴史を概説し,コンピュータに関連する分野の学問について述べる.また現代のデジタル計算機が用いられている機器についても解説する。 |
| 第 10 回 | 【コンピュータII】 コンピュータ特にCPUの歴史について概説し,また現在広く使われているコンピュータの基本構成を解説する。 |
| 第 11 回 | 【ロボット】 現代社会では,ロボットは産業用ロボットをはじめ広く応用されている.ここでは,制御工学からロボット工学について概説し,関連する学問分野との関係を紹介する。 |
| 第 12 回 | 【マイクロ・ナノエレクトロニクス】 半導体分野では,ムーアの法則に従って劇的な技術が進歩している.今後重要となるナノエレクトロニクスについて概説し,関連分野として広がるMEMS等についても解説する。 |
| 第 13 回 | 【電気エネルギー】 発電システムや電気エネルギーの伝送方法,モータ等の電気機器について概説する。 |
| 第 14 回 | 【最近のトピック】 近年におけるトピックを取り上げ,そこでの技術や応用分野,また実用化への道筋について解説する。 |
| 第 15 回 | まとめ (ア)電気電子工学における分野および関連科目についてまとめる |
■科目名:線形代数学(担当:間下 克哉 教授)
◎ 授業の概要
中学校では2元連立一次方程式の,高等学校では3元連立一次方程式の解き方を習います.未知数の個数がささらに増えて4元,5元連立一次方程式・・・となったときどのようにこれを解けば良いでしょう。基本的な考え方は中学校で習う「未知数の消去」ですが,3元連立一次方程式でも,ただ一組の解を持つもの,無数に解を持つもの,解が無いものがあり,多元連立一次方程式を解くためには理論的な裏付けが必要になります。私が担当する線形代数学では,様々な場面で利用される連立一次方程式を解く上でも基礎となる技能と理論をわかりやすく講義しています。
◎ 授業内容
| 第 01 回 | 行列 行列についての基本的な用語 |
|---|---|
| 第 02 回 | 行列の積 行列の積,分割した行列による積 |
| 第 03 回 | 正則行列 単位行列,正則行列 |
| 第 04 回 | 連立方程式 消去法と基本変形 |
| 第 05 回 | 逆行列 逆行列の計算 |
| 第 06 回 | 連立方程式(2) 連立方程式の解と解法 |
| 第 07 回 | 行列の階数 階数の定義と求め方 |
| 第 08 回 | 行列式 行列式の定義,サラスの公式 |
| 第 09 回 | 行列式の性質 多重線形性,転置不変性 |
| 第 10 回 | 余因子展開 余因子展開 |
| 第 11 回 | 余因子展開の応用 逆行列の公式,クラーメルの公式 |
| 第 12 回 | 複素数平面 複素数の絶対値・偏角,複素数平面 |
| 第 13 回 | 平面の方程式 平面の方程式,外積 |
| 第 14 回 | 総合演習 講義の総まとめとして演習を行う |
| 第 15 回 | 予備日 講義内容に対する時間不足への対応など |

